Постоянный ток

В этом разделе изучается направленное движение электрических зарядов.

Понятие об электрическом токе

Электрическим током называется упорядоченное движение электрических зарядов. Условиями существования электрического тока являются:

1) наличие свободных зарядов в проводнике;

2) наличие электрического поля внутри проводника.

Проводниками являются металлы, растворы, расплавы электролитов, газы.

В металлах носителями зарядов являются свободные электроны. В растворах и расплавах электролитов ток обусловлен движением ионов обоих знаков. В газах носителями зарядов являются ионы и электроны.

Под действием электрического поля положительные заряды перемещаются по полю (вдоль вектора ), отрицательные — против поля (против вектора ). Полный ток определяется как сумма токов, образованных носителями каждого знака. Независимо от знака носителей зарядов, за направление тока условно принято направление движения положительных зарядов.

Сила и плотность тока

Основной характеристикой тока является сила тока.

Силой тока называется скалярная величина, равная отношению величины заряда, протекающего через поперечное сечение проводника за некоторый интервал времени, к величине этого интервала.

Для постоянного тока, т. е. тока, не изменяющегося со временем, справедлива следующая формула

В общем случае, если ток переменный, то сила тока вычисляется как производная от заряда по времени:

Плотностью тока называется вектор, величина которого равна отношению силы тока, протекающего через элементарную площадку, перпендикулярную направлению движения зарядов, к площади этой площадки:

Единица плотности тока — А/м² . Вектор плотности тока направлен в сторону движения положительных электрических зарядов.

Плотность тока может быть выражена через концентрацию носителей заряда n и среднюю скорость их упорядоченного движения 

где  e  — заряд одного носителя.

Закон Ома для однородного участка цепи

Закон, устанавливающий связь между силой тока в проводнике и разностью потенциалов (напряжением) на его концах, был открыт Г. Омом опытным путем в 1826 году.

Закон Ома формулируется следующим образом.

Сила тока, текущего по однородному участку цепи, прямо пропорциональна приложенному напряжению и обратно пропорциональна сопротивлению проводника,

Эту формулу еще называют законом Ома в интегральной форме. Напомним, что в случае однородного участка цепи напряжение равно разности потенциалов

Сопротивление проводника зависит от материала и его геометрических размеров, т. е.

где l — длина проводника, S — площадь его поперечного сечения, ρ — удельное сопротивление проводника, которое зависит от рода вещества, а также от его состояния (в первую очередь, температуры). Например, при температуре 20^oС удельное сопротивление меди

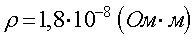
а у фарфора 

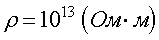
Единицей сопротивления служит ом (Ом), .

Закон Ома справедлив для широкого класса материалов: металлов, угля, электролитов. Его широко применяют для расчета различных электрических цепей. Его используют во многих других случаях, например, в технике безопасности. Так, допустимое напряжение определяют, исходя из сопротивления тела человека и допустимого для него значения тока. Смертельным считается ток 100 мА. Наиболее опасный путь его прохождения: правая рука — ноги. Сопротивление тела при влажной коже   ,   при сухой  . Рассчитайте самостоятельно допустимое напряжение.

Закон Ома в дифференциальной форме

Закон Ома в дифференциальной форме справедлив для любой точки участка цепи как с постоянным, так и с переменным сечением.

Для однородного участка цепи плотность тока равна

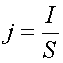
отсюда:     

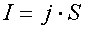
Подставим эту формулу, а также формулу для сопротивления в закон Ома

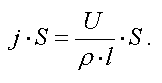
Учтем, что для однородного поля справедлива формула

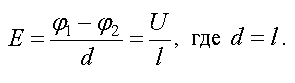
Тогда

Величина, обратная удельному сопротивлению, называется удельной проводимостью, т. е.

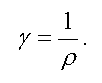
В векторной форме формулу можно записать следующим образом

Формула выражает закон Ома в дифференциальной форме. Плотность тока пропорциональна напряженности электрического поля и имеет одинаковое с ней направление.

В такой форме закон Ома выражает связь между величинами, относящимися к данной точке, и поэтому применим к неоднородным проводникам.

Объяснение закона Ома

Задача физики — выяснить природу явлений, описываемых физическими законами.

Для объяснения закона Ома в начале XIX в. была разработана классическая теория электропроводности металлов. Согласно классическим представлениям, электроны проводимости в металлах образуют так называемый электронный газ. Подобно молекулам идеального газа электроны в металле участвуют в хаотическом движении. При приложении электрического поля на хаотическое движение электронов накладывается упорядоченное движение. Среда оказывает сопротивление движению зарядов в определенном направлении. Поэтому в однородном веществе при постоянной напряженности поля  заряды движутся с постоянной скоростью , пропорциональной напряженности поля

где μ — подвижность носителей, которая зависит от природы носителей, плотности и состояния вещества.

Подставим формулу и получим закон Ома в дифференциальной форме

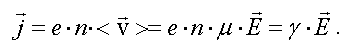
Основанная на этих представлениях классическая теория электропроводности помогла понять и объяснить ряд физических явлений. Но следует отметить, что некоторые экспериментальные факты (например, сверхпроводимость металлов, зависимость сопротивления от температуры, значение их теплоемкости и др.) можно объяснить только с помощью квантовой теории. Однако, классическая теория электропроводности не утратила своего значения и в наши дни, так как во многих случаях (например, при малой концентрации электронов проводимости и высокой температуре, как это имеет место для полупроводников) она дает правильные результаты.

Задачи:

1. За одну минуту через поперечное сечение проводника прошел заряд 180 Кл. При этом первые 20 с сила тока равномерно возрастала от нуля до некоторой величины I₀, затем 30 с не менялась, а последние 10 с равномерно уменьшалась до нуля. Найдите I₀.
2. Плотность тока в проводнике сечением 0,5 мм² равна 3,2 мА/м². Сколько электронов проходит через поперечное сечение проводника за 1 мин?
3. К концам медного провода длиной 200 м приложено напряжение 18 В. Определить среднюю скорость упорядоченного движения электронов проводимости в проводнике, зная, что концентрация электронов проводимости в нем составляет 3·10²³ см^-3.
4. Удлинитель длиной 30 м сделан из медного провода диаметром 1,3 мм. Каково сопротивление удлинителя?
5. Определить силу тока, проходящего через сопротивление 15 Ом, если напряжение на нем составляет 21 В.
6. Какое напряжение надо приложить к концам стального проводника длиной 30 см и сечение 1,5 мм2, чтобы получить ток 10 А?
7. Источник тока с ЭДС 18 В имеет внутреннее сопротивление 6 Ом. Какой ток потечет через сопротивление 30 Ом, подсоединенное к этому источнику?
8. Кислотный аккумулятор имеет ЭДС 2 В, а внутреннее сопротивление 0,5 Ом. Определить силу тока при коротком замыкании.
9. К источнику тока с ЭДС 12 В и внутренним сопротивлением 2 Ом подсоединили параллельно два проводника сопротивлением 10 и 50 Ом. Найти напряжение на зажимах источника.
10. Найти массу алюминиевого провода, из которого изготовлена линия электропередачи длиной 500 м, если при токе 15 А на концах линии возникает разность потенциалов 10 В.

Задания и вопросы для самоконтроля

1. Постоянный электрический ток. Условия существования электрического тока.
2. Сила тока. Формула. Единица измерения.
3. Плотность тока. Формула. Единица измерения.
4. Закон Ома для участка цепи. Определение. Формула.
5. Сопротивление. Формула. Единица измерения.
6. Удельное сопротивление. Формула. Единица измерения.
7. Закон Ома в дифференциальной форме. Определение. Формула.
8. Объяснение закона Ома в дифференциальной форме.