Молекулярная физика и термодинамика — разделы физики, изучающие макроскопические процессы в телах, состоящих из огромного числа частиц — атомов и молекул. У них общий объект изучения, но различные методы. Молекулярная физика изучает свойства тел на основе рассмотрения их молекулярного строения. Термодинамика не обращается к атомно-молекулярному строению вещества, а исходит из нескольких фундаментальных законов (называемых началами термодинамики), которые получены путем обобщения большого количества опытных фактов.
Молекулярно-кинетические представления
Молекулярная физика изучает строение вещества, исходя из молекулярно-кинетических представлений, основывающихся на том, что все тела состоят из молекул, находящихся в непрерывном хаотическом движении. Идея об атомном строении вещества высказана впервые древнегреческим философом Демокритом (460 — 370 гг. до н. э.). Во время прогулки по берегу моря он наблюдал увлажнение одежды и пришел к выводу, что тела состоят из мельчайших неделимых частиц — атомов. В течение многих веков учение об атомах запрещалось церковью. Вновь атомистика возрождается лишь в XVII в. в трудах М.В. Ломоносова. Строгое развитие эта наука получила в XIX в. и связана с работами Клаузиуса, Максвелла, Больцмана и др.
Для построения молекулярно-кинетической теории надо знать размеры атомов. Оценки показывают, что размеры атомов порядка нескольких ангстрем. Ангстрем — это внесистемная единица длины, .
Число атомов или молекул в любом макроскопическом теле огромно. Например, найденное опытным путем число атомов в 12 г изотопа углерода 12С равно . Это число называется числом Авогадро.
В молекулярной физике вводится единица количества вещества — моль (в системе СИ).
Один моль — это количество вещества, в котором содержится столько же молекул (или атомов), сколько атомов содержится в углероде массой 0,012 кг. Отсюда следует: в одном моле любого вещества содержится одинаковое число атомов или молекул, это число называется числом Авогадро.
Так как массы атомов очень малы, удобно использовать в расчетах не массы, измеренные в килограммах, а относительные массы. Относительной молекулярной (или относительной атомной) массой называют отношение массы молекулы (или атома) вещества к массы атома углерода. Относительные атомные массы указаны в таблице Менделеева.
Наряду с относительной молекулярной массой в физике и химии используется понятие молярная масса. Молярная масса вычисляется как масса одного моля вещества, выраженная в килограммах (в системе СИ). Например, молекулярная масса воды (Н2О) находится с помощью таблицы Менделеева и равна
М = 1 ∙ 2 + 16 = 18.
Молярная масса воды
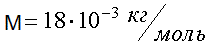
Уравнение состояния идеального газа
Самой простой системой частиц является газ. В то же время его изучение имеет большое практическое значение, хотя бы потому, что газообмен определяет состояние всей биосферы Земли, в том числе человека.
Вместо реального газа, между молекулами которого действуют сложные силы взаимодействия, мы будем рассматривать физическую модель — идеальный газ.
Идеальным газом называется газ, в котором собственными размерами молекул и взаимодействием между молекулами можно пренебречь. Реальные разреженные газы ведут себя подобно идеальному, так как лишь небольшая доля молекул в них находится в состоянии соударения. Например, такие газы, как воздух, кислород, азот и т. д. при комнатной температуре и атмосферном давлении по своим свойствам близки к идеальному.
Состояние заданной массы газа определяется значениями трех термодинамических параметров: давления p, объема V и температуры T. Связь между параметрами называется уравнением состояния. Уравнение состояния идеального газа может быть записано в разных формах.
В наиболее общем виде уравнение состояния идеального газа установили французский ученый Б.П. Клапейрон и русский ученый Д.И. Менделеев. Уравнение Клапейрона-Менделеева имеет вид:
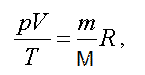
где p — давление; V — объем; T — термодинамическая или абсолютная температура (вычисляется по шкале Кельвина, которая связана с температурой по шкале Цельсия соотношением T = t + 273 ); m — масса вещества, M — молярная масса; R = 8,31(Дж/моль К) — газовая постоянная.
Уравнение Клапейрона — Менделеева формулируется так: произведение давления идеального газа на его объем, деленное на термодинамическую температуру, есть величина постоянная для данной массы газа.
Отношение массы вещества к молярной массе называется количеством вещества

и измеряется в молях.
Уравнению можно придать другой вид. Обозначим через m0 — массу одной молекулы, а N — полное число молекул. Тогда
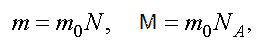
где NA — число Авогадро.

Тогда получим
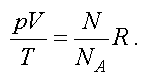
Отношение газовой постоянной к числу Авогадро есть постоянная Больцмана
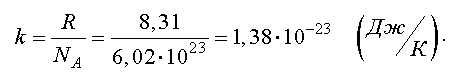
Тогда другая форма записи уравнения состояния идеального газа имеет вид
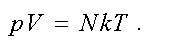
Найдем связь давления и концентрации газа.
Концентрацией называется число молекул, заключенных в единице объема:
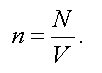
Из этого следует, что давление пропорционально концентрации, т. е.
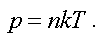
Это еще одна форма записи уравнения состояния идеального газа.
Закон Дальтона для смеси газов
На практике чаще встречаются не чистые газы, а их смеси. Компоненты смеси занимают один и тот же объем и имеют одинаковую температуру. Концентрация смеси равна сумме концентраций компонентов смеси, т. е.
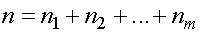
Тогда давление смеси равно
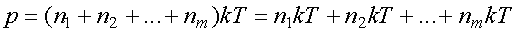
Введем обозначения:
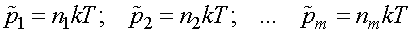
,где
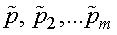
— парциальные давления.
Парциальным давлением называется давление, которое производит на стенки сосуда данная компонента смеси. Тогда давление смеси равно
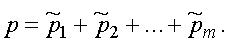
Формула представляет собой закон Дальтона. Давление смеси газов равно сумме парциальных давлений.
Изопроцессы
Состояние идеального газа определяется тремя параметрами: p — давление, V — объем и T — термодинамическая температура. Изменение хотя бы одного параметра приводит к новому состоянию. Для двух различных состояний уравнение Клапейрона — Менделеева имеет вид
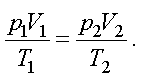
Переход системы из одного состояния в другое называется процессом. Изопроцессом называется процесс, при котором один из параметров остается постоянным. Существует три изопроцесса, законы которых легко получить из уравнения.
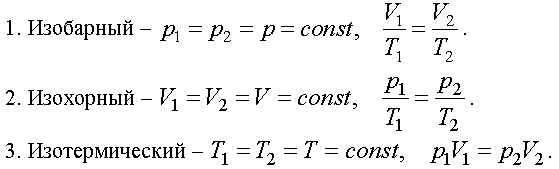
Эти частные законы позволяют связать конечные параметры с начальными.
Молекулярно-кинетический смысл абсолютной температуры
C точки зрения молекулярно-кинетической теории молекулы нагретого тела находятся в хаотическом движении. Причем, чем выше температура T, тем больше средняя кинетическая энергия хаотического движения молекул .
Связь между средней кинетической энергией поступательного движения молекулы и абсолютной температурой дается формулой
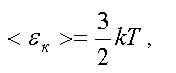
где k — постоянная Больцмана,
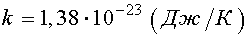
Следовательно, абсолютная температура есть мера средней кинетической энергии поступательного движения молекулы.
Формула позволяет выяснить смысл абсолютного нуля: Т = 0, если
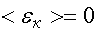
Т. е. абсолютный нуль — это температура, при которой прекращается всякое хаотическое движение молекул.
Давление может быть выражено через среднюю кинетическую энергию поступательного движения молекулы.
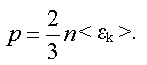
Уравнение называется основным уравнением молекулярно-кинетической теории.
Давление идеального газа равно двум третям средней кинетической энергии поступательного движения молекул, заключенных в единице объема.
Формулы учитывают только кинетическую энергию поступательного движения молекул. Однако, наряду с поступательным движением возможны также вращательное и колебательное движение, поэтому вводится понятие числа степеней свободы.
4.6. Число степеней свободы
Числом степеней свободы механической системы называется число независимых координат, полностью определяющих положение системы в пространстве.
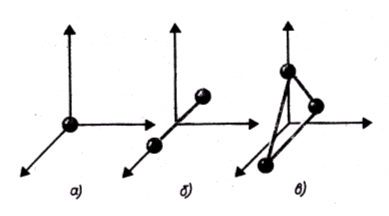
На рис. показаны одноатомная, двухатомная и трехатомная молекулы. Одноатомную молекулу можно представить как материальную точку. Для определения положения точки в пространстве нужно три координаты, т. е. три степени свободы поступательного движения (i = 3).
Молекулу двухатомного газа в первом приближении можно рассматривать как совокупность двух жестко связанных материальных точек. Эта молекула кроме трех степеней свободы поступательного движения имеет две степени свободы вращательного движения (i = 5). Вращение вокруг оси, проходящей через оба атома, не учитывается.
Трехатомная молекула с жесткими связями имеет 6 степеней свободы: 3 — поступательного и 3 — вращательного движения (i = 6).
В классической физике принят постулат о равномерном распределении энергии по степеням свободы. На каждую степень свободы любого вида движения приходится энергия, равная kT/2 . Таким образом, средняя энергия одной молекулы равна
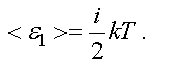
4.7. Внутренняя энергия идеального газа
Внутренняя энергия идеального газа равна суммарной кинетической энергии всех молекул, составляющих систему (напомним, что потенциальной энергией взаимодействия молекул идеального газа пренебрегают),
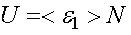
где N — число молекул в системе, которое может быть найдено из формулы.
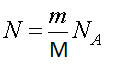
где m — масса газа, μ — молярная масса, NA — число Авогадро.
Следовательно, внутренняя энергия идеального газа равна
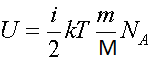
Учтем, что kNA = R — газовая постоянная. Тогда внутренняя энергия идеального газа равна

Изменение внутренней энергии зависит от изменения температуры, т. е.

Внутренняя энергия системы может измениться за счет двух различных процессов: совершения над системой работы A/ и сообщения количества теплоты Q . Заметим, что работа, совершаемая над системой внешними силами, и работа, совершаемая системой против внешних сил, равны по величине и противоположны по знаку: A/ = — A.
Работа в термодинамике
Если в механике работа связана с перемещением тела как целого, то в термодинамике рассматривается перемещение частей тела. Например, если газ, находящийся в цилиндре под поршнем, расширяется, то, перемещая поршень, он производит над ним работу. При этом объем газа изменяется.
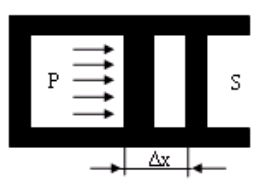
Рассчитаем работу, совершаемую газом при изменениях его объема. Элементарная работа при перемещении поршня на величину dx равна
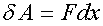
Сила связана с давлением соотношением

где S — площадь поршня.
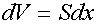
Таким образом

Полную работу A, совершаемую газом при изменениях его объема от V1 до V2, найдем интегрированием формулы

Выражение справедливо при любых процессах
Вычислим работу при изопроцессах:
1) для изохорного процесса V1 = V2 = const, А = 0;
2) для изобарного процесса p = const, A = p(V — V) = pΔV;
3) для изотермического процесса T = const. Из уравнения следует, что
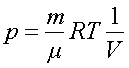
Тогда
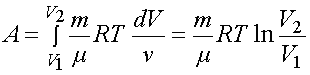
Первое начало термодинамики
Первое начало термодинамики представляет собой обобщение опытных фактов и является по сути дела законом сохранения энергии, примененным к тепловым явлениям.
Первое начало термодинамики имеет несколько формулировок. Одна из формулировок гласит: количество теплоты, переданное системе, идет на изменение внутренней энергии и на совершение системой работы над внешними телами, т. е.

Количество теплоты может быть положительным Q > 0 , если тело получает теплоту, и отрицательным Q < 0 , если тело отдает теплоту.
Первое начало термодинамики показывает, что теплоту можно преобразовывать в работу, т. е. выделять из неупорядоченного движения упорядоченное. Устройство, в котором теплота превращается в работу, называется тепловой машиной. Появление тепловых машин привело к истинной революции в технике и позволило воздвигать различные сооружения, создавать транспортные средства и даже поддерживать связь на расстоянии.
КПД тепловой машины
Тепловые машины могут иметь разную конструкцию. Это может быть паровой двигатель, двигатель внутреннего сгорания, реактивный двигатель. Любой тепловой двигатель работает по замкнутому циклу и имеет нагреватель, рабочее тело двигателя и холодильник. Принципиальная схема тепловой машины приведена на рис.
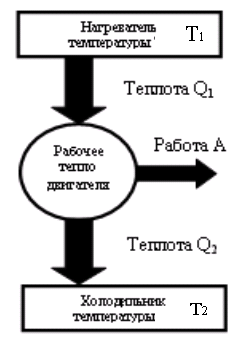
В процессе работы теплового двигателя рабочее тело двигателя получает от нагревателя количество теплоты Q1, совершает работу A и передает холодильнику количество теплоты Q2 < Q1 . Для замкнутого цикла изменение внутренней энергии равно нулю ΔU = 0. Следовательно, согласно I началу термодинамики, работа, совершаемая двигателем, равна
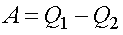
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы, совершаемой двигателем, к количеству теплоты, полученному от нагревателя
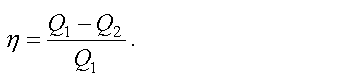
Как показывает формула, КПД тепловой машины всегда меньше единицы

Следовательно, невозможно всю теплоту превратить в работу.
Ученые всегда стремились повысить КПД. В первой половине XIX в. французский ученый Сади Карно показал, что максимально возможное значение КПД тепловой машины равно
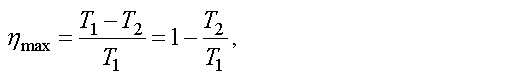
где T1 — температура нагревателя, T2 — температура холодильника.
Повышение КПД тепловых двигателей и приближение его к максимально возможному значению — важнейшая техническая задача. Однако, все тепловые двигатели выделяют большое количество теплоты, что называется тепловым загрязнением, и выбрасывают в атмосферу вредные для растений и животных химические соединения. Это ставит серьезные проблемы охраны окружающей среды.
Второе начало термодинамики. Энтропия
Второе начало термодинамики является фундаментальным законом природы. Оно охватывает самый широкий круг природных явлений и указывает направление, в котором самопроизвольно протекают термодинамические процессы.
Второе начало термодинамики, как и первое, имеет несколько формулировок.
Невозможен круговой процесс, единственным результатом которого является превращение теплоты, полученной от нагревателя, полностью в работу.
Невозможен круговой процесс, единственным результатом которого является передача теплоты от менее нагретого тела к более нагретому.
Эти формулировки показывают, что тепловые процессы являются необратимыми. Мерой необратимости процесса, мерой хаотичности является энтропия.
К определению энтропии S можно прийти на основе анализа работы тепловых машин. Если система получает тепло Q > 0 или отдает тепло Q < 0, то состояние ее меняется. Тогда, при изменении состояния системы, можно найти не саму энтропию, а только ее изменение, т. е.

Для тепловой машины изменение энтропии нагревателя и холодильника равны:
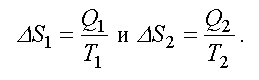
Формула
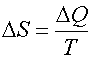
справедлива для изотермического процесса и представляет собой термодинамическое определение энтропии.
Энтропией называется термодинамическая величина, изменение которой в системе пропорционально изменению ее тепловой энергии, деленной на абсолютную температуру.
Найдем изменение энтропии за один цикл для тепловой машины. Полное изменение энтропии за цикл больше или равно нулю

Знак равенства ΔS = 0 относится к обратимым процессам, которые являются бесконечно медленными процессами.
Знак неравенства ΔS > 0 относится к необратимым процессам. В реальных системах все процессы необратимы. Например, расширение газа, выравнивание температуры.
Таким образом, второе начало термодинамики формулируется и как закон возрастания энтропии.
Во всех необратимых процессах в замкнутой системе энтропия всегда возрастает.
Возрастание энтропии сопровождается выравниванием температуры или плотности газа. Это можно связать с порядком и беспорядком. Под порядком будем понимать сосредоточение частиц или энергии в определенном месте пространства, а под беспорядком (хаосом) — равномерное распределение их во всем объеме. Тогда возрастание энтропии при совершающихся без внешних воздействий необратимых процессах отражает природное стремление систем переходить от состояния более упорядоченного в состояние менее упорядоченное. Этот процесс сопровождается рассеянием (или диссипацией) энергии.
Как мы видим, второе начало термодинамики определяет направленность тепловых процессов в изолированных системах, они всегда протекают в сторону роста энтропии, в сторону увеличения беспорядка. Капелька туши растворяется во всем объеме, колечко сигаретного дыма тает, огонь костра гаснет, разрушаются горы, гаснут звезды и т. д. Вся практическая деятельность людей как в технике, так и в сельском хозяйстве, представляет собой не что иное, как создание из природных материалов искусственных структур, т. е. в том или ином смысле борьбу с самопроизвольным ростом энтропии.
Возникновение упорядоченных структур возможно только в незамкнутых, т. е. в открытых системах. Открытой системой называется система, которая обменивается энергией и веществом с окружающей средой. В открытых системах энтропия может как возрастать, так и убывать в зависимости от знака Q/T .
Трудами Ильи Пригожина (датский физик русского происхождения) строго доказано, что в открытых системах, находящихся в неравновесном состоянии, при определенных условиях из хаоса может возникать порядок. Процесс возникновения из хаоса упорядоченных структур называется самоорганизацией. Процессы самоорганизации являются общими для живой и неживой природы.
Феномен жизни является примером сохранения и увеличения упорядоченности и, следовательно, уменьшения энтропии. Жизненный цикл наблюдается только в открытых системах. Он включает в себя три стадии: рождение, развитие, смерть. На первых двух стадиях энтропия понижается, возникает и развивается структура. На этих стадиях живой организм поддерживает связь с окружающей средой. На третьей стадии система становится замкнутой, энтропия возрастает и достигает максимума. В этом смысле жизнь — это борьба с возрастанием энтропии. Человек существует, пока он активно поддерживает связь с окружающим миром, обменивается с ним энергией, веществом и информацией.
Задачи:
- Предельно допустимая концентрация молекул паров ртути (Hg) в воздухе равна 3 · 1016 м -3, а ядовитого газа хлора (Cl2) — 8,5 · 1018 м-3. Найти, при какой массе каждого из веществ в одном кубическом метре воздуха появляется опасность отравления.
- Находившаяся в стакане вода массой 200 г полностью испарилась за 20 сут. Сколько в среднем молекул воды вылетало с ее поверхности за 1 с?
- Во сколько раз изменится давление газа при уменьшении его объема в 3 раза? Средняя скорость движения молекул осталась неизменной.
- Какова средняя квадратичная скорость движения молекул газа, если, имея массу 6 кг, он занимает объем 5 м3 при давлении 200 кПа?
- Найти среднюю кинетическую энергию молекулы одноатомного газа при давлении 20 кПа. Концентрация молекул этого газа при указанном давлении составляет 3 · 1025 м-3.
Задания и вопросы для самоконтроля
- В чем заключается молекулярно-кинетические представления?
- Что такое моль? Как находится молярная масса?
- Запишите уравнение Менделеева — Клапейрона.
- Сформулируйте закон Дальтона.
- Назовите изопроцессы.
- В чем молекулярно-кинетический смысл абсолютной температуры?
- Что называется числом степеней свободы?
- Как вычисляется внутренняя энергия идеального газа?
- Как вычисляется работа в термодинамике?
- Сформулируйте I начало термодинамики.
- Как устроена тепловая машина? От чего зависит КПД тепловой машины?
- Что показывает энтропия? Дайте термодинамическое определение энтропии.
- Сформулируйте II начало термодинамики.
- Как определяется направленность тепловых процессов? Как изменение энтропии связано с порядком и беспорядком?
- Какая система называется открытой?
- Что называется самоорганизацией?
- Как ведет себя энтропия в живых системах?