Колебания

Характеристики колебательного процесса

Колебаниями называются движения или процессы, обладающие той или иной повторяемостью во времени. Колебательное движение — одно из самых распространенных движений в природе и технике. Колеблются деревья в лесу, струны музыкальных инструментов, вагоны на стыках рельсов, в природе наблюдаются приливы и отливы, возникают землетрясения, колеблются атомы в кристаллической решетке и т. д. Физическая природа колебаний может быть различной. Например, качание маятника в часах — это механические колебания, колебания напряжения в сети переменного тока — это электрические колебания. Однако, различные колебательные процессы описываются одинаковыми уравнениями и имеют одинаковые характеристики. Характеристиками колебательного процесса являются: T — период, ν — частота, ω — круговая частота, A — амплитуда, φ — фаза.

Периодом T называется время одного полного колебания.

Частотой ν  называется число колебаний в единицу времени.

Связь между частотой и периодом дается формулой

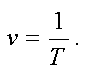
В системе СИ период измеряется в секундах, а частота в герцах, .

Круговой или циклической частотой называется число колебаний за промежуток времени 2π секунд. Связь между круговой частотой ω и частотой ν выражается формулой

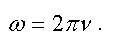
Связь ω с периодом T  дается уравнением

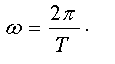
Амплитудой называется наибольшее отклонение (смещение) колеблющейся величины от положения равновесия.

Фазой называется величина, определяющая отклонение (смещение) колеблющейся величины в данный момент времени

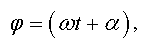
где α — начальная фаза.

Частным случаем периодических колебаний являются гармонические колебания.

Уравнение гармонических колебаний

В природе и технике существует множество самых разнообразных колебаний. Простейшими колебаниями являются гармонические колебания.

Гармоническими колебаниями называются такие колебания, при которых колеблющаяся величина изменяется со временем по закону синуса или косинуса.

Уравнение гармонических колебаний имеет вид

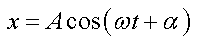
или

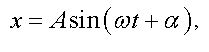
где x — смещение колеблющейся величины от положения равновесия.

Уравнение гармонических колебаний, описываемое формулой (3.5) или (3.6), является решением так называемого дифференциального уравнения гармонических колебаний.

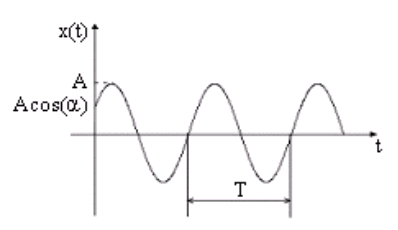
На рисунке представлен график зависимости смещения от времени для гармонических колебаний. На нем показаны амплитуда A и T период .

Скорость и ускорение при гармоническом колебательном движении

Пусть тело совершает колебания вдоль оси х, т. е.

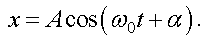
Скорость в этом случае равна производной от координаты по времени

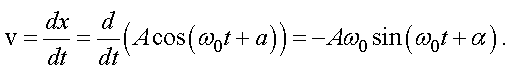
Из этой формулы видно, что скорость тоже меняется по гармоническому закону с амплитудой скорости

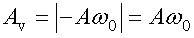
Максимальное значение скорости при гармонических колебаниях равно

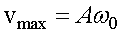
Ускорение равно производной от скорости по времени

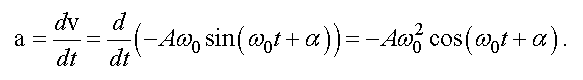
Ускорение тоже меняется по гармоническому закону. Амплитуда ускорения равна

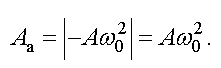
Максимальное значение ускорения при гармоническом колебании равно амплитуде ускорения

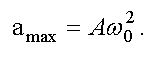
Значение возвращающей силы находится по II закону Ньютона

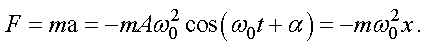
Энергия гармонических колебаний

Колеблющееся тело обладает кинетической и потенциальной энергией.

Кинетическая энергия колеблющейся материальной точки с массой m вычисляется по формуле:

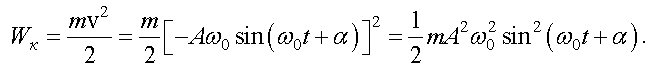
Потенциальная энергия материальной точки, совершающей колебания под действием упругой силы вычисляется по формуле

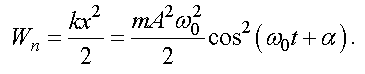
Полная энергия гармонических колебаний равна

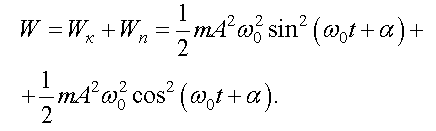
Учитывая, что   

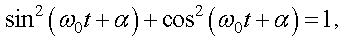
   получим

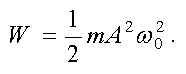
Из формулы следует, что полная энергия при гармонических колебаниях не зависит от времени, т. е. остается постоянной. Следовательно, выполняется закон сохранения механической энергии.

Второй важный вывод: энергия при гармонических колебаниях пропорциональна квадрату амплитуды и квадрату частоты.

Векторная диаграмма

При рассмотрении многих вопросов, в частности, при сложении колебаний одинакового направления и частоты бывает удобно гармоническое колебание представить в виде векторной диаграммы. Векторная диаграмма строится следующим образом: надо изобразить вектор, длина которого равна амплитуде, угол наклона к оси абсцисс равен начальной фазе. Если привести этот вектор во вращение с угловой скоростью ω₀, равной круговой частоте колебаний, то проекция его конца на выбранную ось будет изменяться по гармоническому закону.

На рисунке представлена векторная диаграмма для гармонического колебания

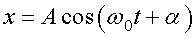
в момент времени t = 0.

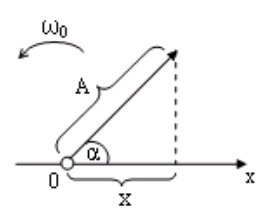
Метод векторных диаграмм удобен при сложении колебаний одинаковой частоты.

Сложение гармонических колебаний одинакового направления и одинаковой частоты

Пусть надо сложить два колебания, которые определяются уравнениями

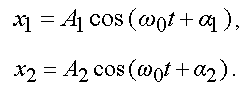
Представим каждое колебание в виде вектора и найдем по правилам сложения векторов результирующий вектор (рис. 3.4).

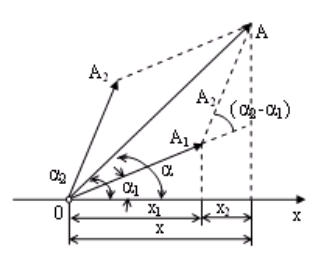
Результирующее колебание равно сумме складываемых колебаний, т. е.

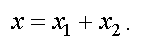
Так как угловая скорость ω₀ у складываемых векторов одинакова, то результирующий вектор тоже вращается со скоростью ω₀. Тогда уравнение результирующего колебания имеет вид

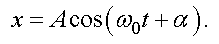
Результирующую амплитуду можно найти по теореме косинусов

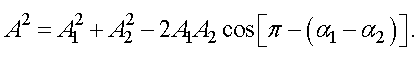
По формулам приведения в тригонометрии

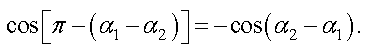
Тогда квадрат результирующей амплитуды равен

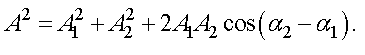
Результирующая амплитуда равна

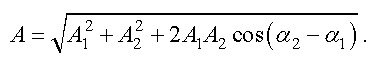
Проанализируем выражение для амплитуды. Это выражение показывает, что значение амплитуды результирующего колебания зависит от разности фаз складываемых колебаний.

Если разность фаз (α₂ — α₁) = 2nπ, где n = 0, 1, 2, …, то A = A₁ + A₂ — это максимальное значение для результирующей амплитуды. Если разность фаз (α₂ — α₁) = (2n+1)π, где n = 0, 1, 2, …, то A = A₁ — A₂ — это минимальное значение амплитуды. Следовательно, колебания в зависимости от разности фаз могут усиливать или ослаблять друг друга. Этот важный вывод используется при описании интерференции волн.

Задачи:

1.  Грузик, колеблющийся на пружине, за 8 с совершил 32 колебания. Найти период и частоту колебаний.
2. Частота колебаний крыльев комара 600 Гц, а период колебаний крыльев шмеля 5 мс. Какое из насекомых сделает при полете больше взмахов крыльями за 1 мин и на сколько?
3.  Груз массой 400 г совершает колебания на пружине жесткостью 250 Н/м. Амплитуда колебаний 15 см. Найти полную механическую энергию колебаний и наибольшую скорость движения груза.
4.  Во сколько раз изменится частота колебаний математического маятника при увеличении длины нити в 3 раза?
5. Во сколько раз изменится полная механическая энергия колеблющегося маятника при уменьшении его длины в 3 раза и увеличении амплитуды колебаний в 2 раза?
6. Определить по графику, приведенному на рисунке амплитуду, период и частоту колебаний.

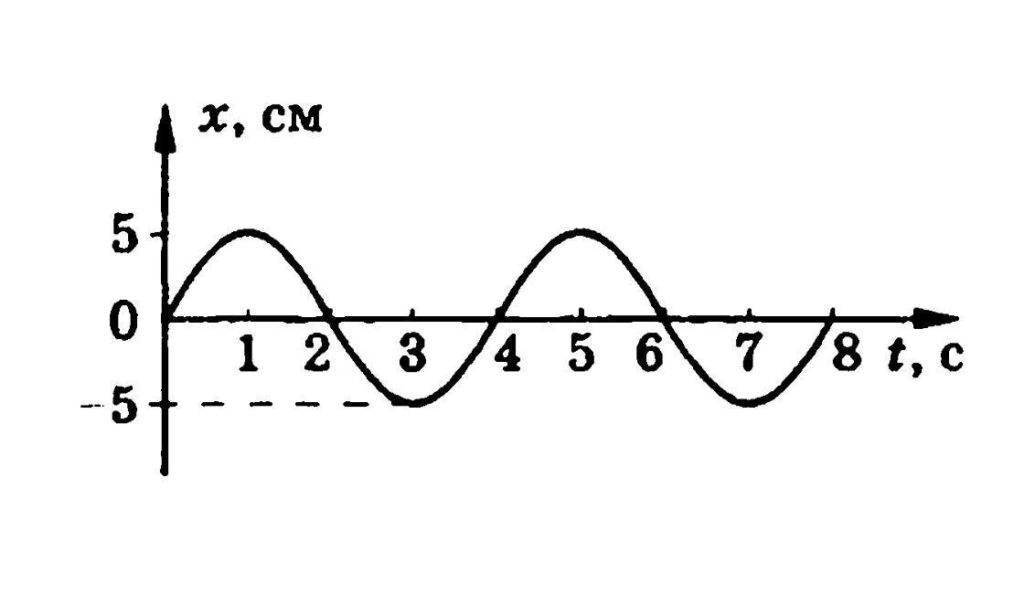
7. Найти массу груза, который на пружине жесткостью 250 Н/м делает 20 колебаний за 16 с.

8. Если к некоторому грузу, колеблющемуся на пружине, подвесить гирю массой 100 г, то частота колебаний уменьшится в 1,41 раза. Какой массы груз был первоначально подвешен к пружине?

9. Во сколько раз изменится период колебаний груза, подвешенного на резиновом жгуте, если отрезать 3/4 длины жгута и подвесить на оставшуюся часть тот же груз?

10. Во сколько раз изменится полная механическая энергия колеблющегося маятника при уменьшении его длины в 3 раза и увеличении амплитуды колебаний в 2 раза?

Задания и вопросы для самоконтроля

1. Что называется колебаниями?
2. Дайте определение периода, частоты, фазы, циклической частоты, амплитуды.
3. Какие колебания называются гармоническими?
4. Составьте дифференциальное уравнение гармонических колебаний на примере пружинного маятника.
5. Как вычислить скорость и ускорение гармонических колебаний?
6. От чего зависит энергия гармонических колебаний?
7. Как строится векторная диаграмма?
8. Как сложить два гармонических колебания одинакового направления и частоты? От чего зависит результирующая амплитуда?