Основанный Александром Македонским город Александрия в дельте Нила стал благодаря своему выгодному географическому положению средоточием торговых связей, будучи при этом столицей Египта. Александрия во II – I веках до н. э. была огромным городом, насчитывавшим сотни тысяч человек свободного населения и гораздо большее количество рабов.
Переходя к подробному изложению развития астрономии в эллинистическую эпоху, следует еще раз напомнить о том, что результаты трудов вавилонских жрецов должны были стать известны греческим астрономам. В государстве Селевкидов, образовавшемся на территории Персии, завоеванной Александром Македонским, сохранялась вавилонская культура и продолжались наблюдения за небесными светилами. По сообщениям древих авторов, вавилонский жрец Борог ( 275 г. до н. э.), написавший исто- рию Вавилонии, переехав в Грецию, возможно, сообщил греческим ученым о многих полученных в Вавилоне астрономических результатах.
Достигнутые греческими астрономами успехи в создании теорий движения небесных тел, позволяющих предсказывать различные явления, в большой мере были обусловлены развитием в эллинистическую эпоху математики. Особо важными были труды Евклида ( 300 г. до н. э.), Аполлония Пергамского ( 230 г. до н. э.) и Архимеда ( 216 г. до н. э.), выработавших и использовавших метод решения геометрических задач на строго логических основаниях. Знаменитое сочинение Евклида «Начала» содержит настолько полное изложение этого метода, что на протяжении двух тысячелетий оно не нуждалось в дополнениях и изменениях. Этот метод использовался при решении астрономических задач вплоть до XVII века — Птолемеем, арабскими астрономами, Коперником и Ньютоном.
Система мира, созданная Аристотелем, и в эллинистическую эпоху принималась большинством философов как единственно правильная, хотя высказывались и иные взгляды по поводу характера наблюдаемых на небе движений. Так, в частности, современник Аристотеля Гераклид Понтийский (388–315 гг. до н. э.) и некоторые другие философы считали суточное вращение небесного свода лишь видимым следствием вращения Земли. Ссылки на не дошедшие до нашего времени труды Гераклида дают основание считать, что он объяснял особенности движения Меркурия и Венеры вращением этих планет не вокруг Земли, а вокруг Солнца, которое само вращается вокруг Земли.
Совершенно иное место в системе мира отводилось Солнцу Аристархом Самосским (310–230 гг. до н. э.), который, также впервые в истории астрономической науки поставив задачу об определении расстояний до Солнца и Луны, предложил метод ее решения и сам пытался найти расстояния из наблюдений. Этим вопросам посвящено единственное дошедшее до нас сочинение Аристарха «О размерах и расстояниях Солнца и Луны». Он основывался на известных к тому времени представлениях о том, что Луна вращается вокруг Земли и получает свой свет от Солнца. Затмение Лу- ны происходит при погружении ее в тень Земли. При видимости половины Луны ее угловое расстояние от Солнца «меньше прямого угла на 1/30 его часть». На этой основе путем применений геометрических теорем Аристархом были получены для величины неравенства для оценки отношения расстояния до Солнца rⓈ к расстоянию до Луны rC: 18 < rⓈ < 20. Аристарх, как и другие математики того времени, не использовал числа 19, о, поскольку sin 3◦ ≈ 1 , то rⓈ = 19. Это значение и применяется далее при записи соотношений между расстояниями и диаметрами, выведенных Аристархом.
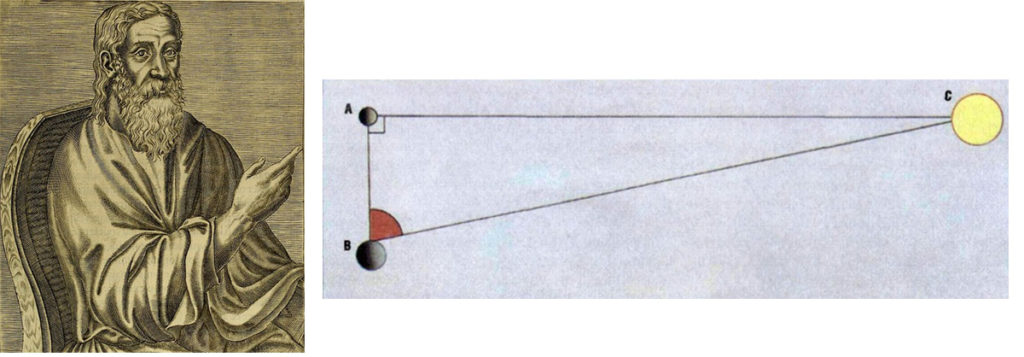
Таким образом, Аристарх внес важнейший вклад в науку, впервые оце- нив расстояния до небесных светил. Расстояние до Солнца, полученное им, долгое время — до XVIII века — принималось астрономами. Кроме того, он создал гелиоцентрическую систему мира, за что его назвали «Коперником древности». Такое название не вполне точно, поскольку главное достижение Коперника состояло в использовании понятия относительности движения для объяснения видимого движения планет, что Аристарху было чуждо.
Первое точное определение радиуса Земли на основе астрономических наблюдений было сделано Эратосфеном (276–194 гг. до н. э.) — географом и астрономом, одним из первых заведующих Александрийской библиотекой. Им было использовано то обстоятельство, что Александрия и город Сиена (ныне г. Асуан) находятся практически на одном меридиане. В день лет- него солнцестояния Солнце в Сиене находится в зените, а в Александрии в то же время его отклонение от зенита составляет 1/50 полной окружности. Этому значению разности высот соответствует измеряемое расстояние между городами, равное 5 000 стадиям (греческая мера длины, предположительно равная 157 м). Таким образом, длина окружности Земли получится равной 25 000 стадиям, что близко к ее современным определениям. В сочинениях древних авторов содержатся сведения о том, что Посидоний (135–51 гг. до н. э.) определял размеры Земли аналогичным методом, используя наблюдения разности высот яркой звезды Канопус. Когда на острове Родос звезда находилась на горизонте, в Александрии ее высота над горизонтом составляла 7◦.5. Результат определения размера Земли таким путем оказался близким к полученному Эратосфеном.

Эратосфену принадлежит много сочинений, среди которых «География», «Хронография», «Измерение Земли», не дошедшие до нашего времени. С его именем связывают также определение угла наклона эклиптики к экватору, для которого было получено значение (в долях окружности) 11/83, что в градусной мере составляет 23◦ 51′.
Крупнейшим астрономом эллинистического периода считают Гиппарха

(185–126 гг. до н. э.), работавшего в обсерватории на острове Родос, который в то время был независимым и имел демократическую форму правления. Трактаты Гиппарха «О длине года», «Об интеркаляции месяцев и дней», «Об изменении солнцестояний и равноденствий» не сохранились и результаты его трудов стали известны только благодаря сочинению «Альмагест», принадлежащему Клавдию Птолемею (середина II в. н. э.). Содержание этого труда будет подробно изложено далее (полное его название «Тринадцать книг математического сочинения», название «Альмагест» дано при переводе арабами). Как сообщает Птолемей, Гиппарх был хорошо знаком с результатами наблюдений движения Луны, затмений и других явлений, проводившихся ранее вавилонскими жрецами. Гиппарх уточнил среднюю продолжительность лунного месяца, получив величину, всего на 1s отличающуюся от современного значения.
Между 162 и 128 г. до н. э. Гиппарх наблюдал девять солнцестояний и сравнивал результаты с данными наблюдений Аристарха, проводившихся более чем на сто лет ранее. Это сравнение привело его к выводу о том, что промежуток времени от одного солнцестояния (или равноденствия) до следующего такого же («тропический год») отличается от промежутка времени, по истечении которого Солнце занимает прежнее положение среди звезд (сидерический период обращения Солнца, или «звездный год»). По Гиппарху, продолжительность тропического года составляет 365d5h55m12s (это более чем на 6m ошибочно). По Гиппарху, различие между тропическим и звездным годами равно приблизительно 20m и объясняется смещением точки весеннего равноденствия вдоль эклиптики в сторону, противоположную направлению движения Солнца. Величина этого смещения, названного прецессией («предварением»), по Гиппарху, равна 0◦.01 в год. Вследствие прецессии меняется только долгота, но не широта звезд.
Отличие величины, полученной Гиппархом, от современной связано, возможно, с неточностью наблюдений, которые, как полагают, выполнялись посредством «экваториального кольца». При таких наблюдениях высота светила определяется по наклону кольца в момент, когда светило видно сквозь диаметрально противоположные отверстия в кольце.
Смелым шагом на пути развития астрономических знаний был отказ от устойчивого представления о положении Земли в центре окружности, по которой равномерно обращается Солнце. Неравномерность движения Солнца по эклиптике была обнаружена еще до Гиппарха — весной и летом оно движется быстрее, а осенью и весной — медленнее. Гиппарх, сохранив предположение о равномерности движения Солнца по окружности (как и других светил по своим кругам), сместил Землю в некоторую точку, придав ей таким образом эксцентрическое положение. При движении Солнца его расстояние от Земли должно изменяться — медленнее всего оно движется при наибольшем удалении, в апогее, а наибольшую скорость имеет в ближайшем к Земле положении — в перигее. Окружность, по которой происходит движение, называется эксцентром, а скорость этого движения представляет собой среднее за год ее значение. Долготы Гиппархом отсчитывались от точки весеннего равноденствия. Расстояние Земли от центра окружности — эксцентриситет — было оценено Гиппархом в 1/24 ее радиуса, а для долготы точки апогея было получено значение 65◦30′. Указанным путем Гиппарх смог учесть действительную неравномерность движения Земли вокруг Солнца, обусловленную эллиптичностью земной орбиты. Использование геометрической модели для объяснения наблюдаемых неравенств движения Солнца продемонстрировало прогресс науки в эллинистическую эпоху по сравнению с вавилонской астрономией.
Для истолкования неравномерности видимого движения Луны Гиппарх также использовал метод введения эксцентра. Он пытался находить изменения видимых размеров Луны и Солнца, вызванные движением по эксцентру. Для определения углового диаметра светил использовалось специальное устройство — рейка с движущимися визирами.
Использовав результаты наблюдений затмений, проведенных в Вавилоне, Гиппарх смог значительно уточнить соотношение между продолжительностями синодического и сидерического лунных месяцев, а также определить период обращения точки перигея Луны по орбите, оказавшийся равным примерно девяти годам. Было также установлено, что эксцентр наклонен к эклиптике под углом 5◦. По продолжительности лунного затмения и величине углового диаметра Луны Гиппарх находил параллакс Луны.
Им использовался также другой способ решения этой задачи — по разности фаз солнечного затмения в двух местах, широта которых известна — в Александрии и Геллеспонте. При этом было получено, что rC 57RC.
До настоящего времени не потерял значения составленный Гиппархом каталог звезд (около 850 звезд) с указанием их эклиптических координат и оценки видимого блеска (звездной величины). Этот каталог с добавлением 170 звезд и с поправками долгот за прецессию приведен Птолемеем в «Альмагесте». Об инструментах, которыми пользовался Гиппарх при наблюдениях звезд, вошедших в каталог, ничего не сказано, но, возможно, это была армиллярная сфера.

Не исключено, что составление Гиппархом каталога стимулировалось наблюдениями им вновь появлявшихся звезд (новых или переменных).
Кинематическая схема движения Солнца и Луны, предложенная Гиппархом, позволяет рассчитывать движение этих тел и предсказывать их положение. Методика таких расчетов воспроизведена Птолемеем в «Альагесте».
«Второе неравенство» видимого движения планет заключается в наличии петель в их путях. Планеты Марс, Юпитер и Сатурн сначала отстают от Солнца и после «стояния» движутся попятным движением (от востока к западу) до следующего стояния. Меркурий и Венера обгоняют Солнце, двигаясь к востоку, затем останавливаются и, двигаясь попятно, отстают от Солнца, но затем снова догоняют его.
Для объяснения сложного видимого движения планет Птолемей использовал понятие эпицикла. Планета предполагается движущейся по окружности (эпициклу) с угловой скоростью σ, а центр эпицикла движется по другой окружности (деференту) с угловой скоростью ω (рис. 13).
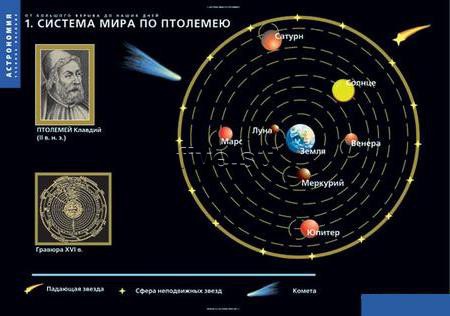
Понятие эпицикла впервые встречается у геометра Аполлония Пергамского (около 200 г. до н. э.), доказавшего теорему о возможности замены эксцентрического движения равномерным эпициклическим движением. Теорию эпициклов далее развивал Гиппарх. Птолемей ее усовершенствовал и применил для объяснения движения планет, использовав данные наблюдений. При этом он выдвинул два постулата:
Постулат 1. Приходя в соединение с Солнцем, каждая из верхних планет одновременно приходит в апогей своего эпицикла и достигает наибольшего удаления от наблюдателя.
Постулат 2. Пусть ω3, ω4, ω5 — средние скорости движения центра эпицикла по деференту, σ3, σ4, σ5 — синодические скорости движения (по эпициклу), µ — среднее суточное движение Солнца по долготе. Тогда ω3 + σ3 = ω4 + σ4 = ω5 + σ5 = µ.
Как утверждается в «Альмагесте», эти условия выполняются с очень высокой точностью (до «сексты градуса», т. е. до 16 доли градуса).
Приведем высказывание известного астронома и историка науки Н. И. Идельсона о роли разработанной и примененной Птолемеем теории движения планет: «Древняя система описывала математическую картину реального мира. “Альмагест” — отнюдь не бредни варвара и не грезы пифагорейцев, это истинная теоретическая астрономия». Теория Птолемея имела важнейшее значение не только для практических приложений астрономии, но и для дальнейшего развития науки. Она распространялась как элемент античной культуры и за пределы эллинистического мира. В частности, около 400 г. н. э. в Индии появился трактат «Сурья Сиддханта» с изложением теории эпициклов и ее применений. В VI веке получило распространение сочинение Варах Махири «Панга Сиддхантика», в котором давалось упрощенное изложение теорий Гиппарха и Птолемея.