Иоганн Кеплер родился в 1571 году. Закончил Тюбингенскую духовную академию. После окончания занимался преподаванием.

Книга «Предвестник космографических изысканий, содержащий космографическую тайну об удивительном соотношении небесных сфер, а также истинные и должные причины числа небес, их величин и периодических их движений, объяснённую посредством пяти правильных геометрических тел» показала большие математические способности и послужила сближению Кеплера с Тихо Браге. В дальнейшем И. Кеплер вывел свои законы на основании наблюдений, собранных Тихо Браге.
В 1609 году вышла в свет книга «Новая астрономия, причинно обоснованная, или физика неба, изложенная в исследованиях движения звезды Mapc, по наблюдениям благороднейшего мужа Тихо Браге». В этой книге формулировались первые два закона движения небесных тел. Третий закон появился спустя 10 лет исследований в книге «Гармония мира», вышедшей в 1619 году. Долгие годы исследований заставили Кеплера отречься от прежних идеализированных воззрений на природу движения небесных тел.
Законы Келлера формулируются следующим образом:
1 закон Кеплера (1616 г.)
Все планеты движутся по эллипсам, в одном из фокусов которых находится Солнце.
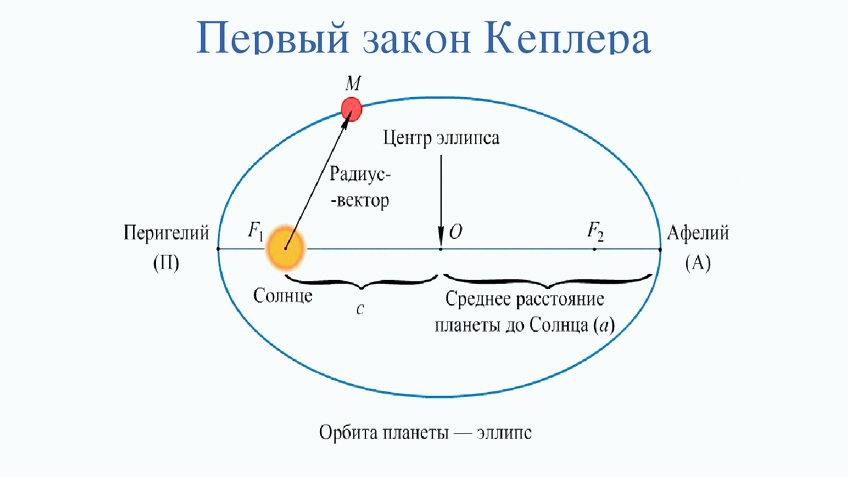
2 закон Кеплера
Радиус — вектор планеты в равные промежутки времени описывает равновеликие площади.
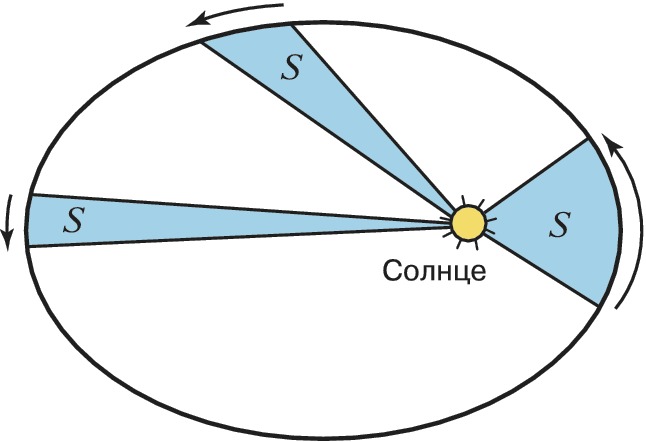
3 закон Кеплера
Квадраты сидерическим периодов обращений планет вокруг Солнца пропорциональны кубам больших полуосей их эллиптических орбит.
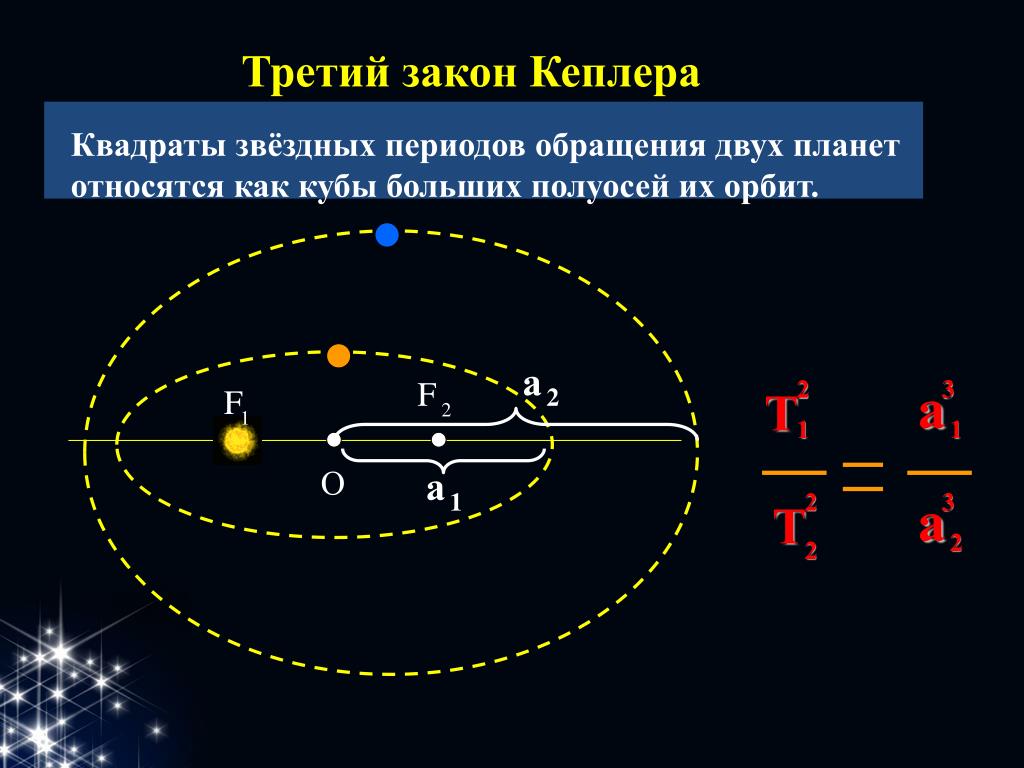
где T1, T2 — сидерические периоды обращений планет, a1, a2 — большие полуоси их орбит. Если большие полуоси орбит выражать в единицах среднего расстояния от Земли до Солнца (в а.е.), а периоды обращений в годах, то для Земли а =1, Т = 1, и тогда для любой планеты вокруг Солнца будет справедливо уравнение:
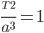
Движение планет происходит по законам Кеплера. Законы объясняют неоднородное перемещения космических тел с их помощью можно рассчитать массу тел.
Законы движения планет равносильны правилам движения спутников, в том числе и искусственных. Благодаря знаниям закономерностях движения небесных объектов, стал возможным запуск космических ракет. Кеплер внёс огромный вклад в развитие астрономии.
Годичный параллакс и расстояния до звёзд
Мысли о том, что звёзды — это далёкие солнца, высказывались ещё в глубокой древности. Однако долгое время оставалось неясным, как далеко они находятся от Земли. Ещё Аристотель понимал, что если Земля движется, то, наблюдая положение какой-либо звезды из двух диаметрально противоположных точек земной орбиты, можно заметить, что направление на звезду изменится. Это кажущееся (параллактическое) смещение звезды будет служить мерой расстояния до неё: чем оно больше, тем ближе к нам расположена звезда. Но не только самому Аристотелю, но даже значительно позднее Копернику не удалось обнаружить это смещение. Только в конце первой половины XIX в., когда телескопы были оборудованы приспособлениями для точных угловых измерений, удалось измерить такое смещение у ближайших звёзд.
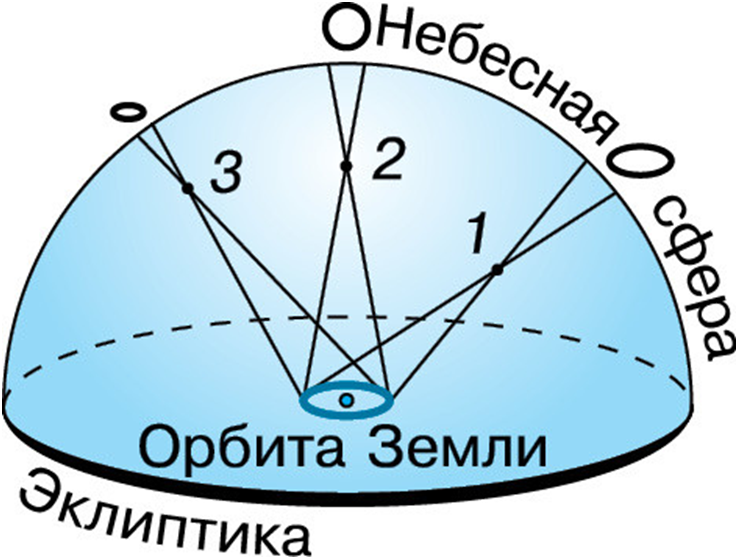
Рис. Параллактическое смещение звезды
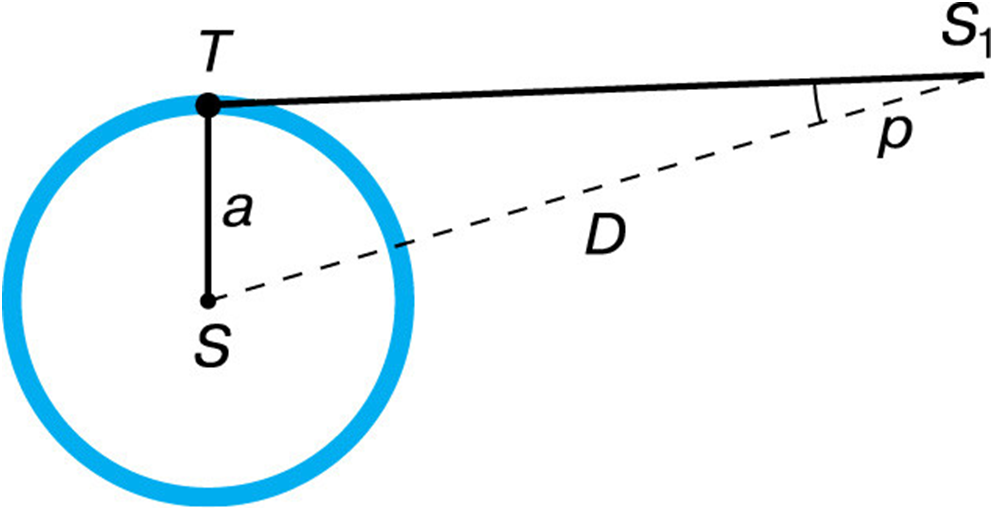
Рис. Годичный параллакс звезды
Годичным параллаксом звезды p называется угол, под которым со звезды можно было бы видеть большую полуось земной орбиты (равную 1 а. е.), перпендикулярную направлению на звезду.
Расстояние до звезды
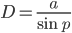
где a — большая полуось земной орбиты. Заменив синус малого угла величиной самого угла
p = sin p, выраженной в радианной мере, и что 1 рад = 206 265″ и приняв a = 1 а. е. = 149,6 млн. км, получим следующую формулу для вычисления расстояния до звезды:
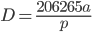
В астрономии за единицу расстояний до звёзд принята величина принята величина 1 парсек(пк)
1 пк = 206265 а = 3 х 1016м = 3,26 св.г.
Тогда расстояние до ближайшей звезды Проксимы альфа-Центавра, параллакс которой составляет p = 0,75«
Тогда
D = 1/р = 1/0,75 =1,33 пк = 4,3 св.г.